Station - Zählschleifen

Zählschleifen

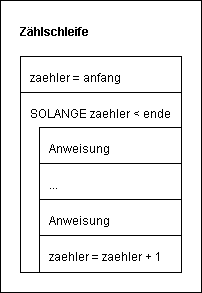
Bei einer Zählschleife durchläuft der Wert einer Zählvariablen einen Zahlenbereich von einem Anfangswert bis zu einem Endwert. Für jeden Wert der Zählvariablen wird die angegebene Anweisungssequenz einmal ausgeführt.

Jede Zählschleife lässt sich durch eine Solange-Wiederholungsanweisung ersetzen.

Aufgabe 1

(a) Ergänze und konkretisiere die beiden gezeigten Struktogramme so, dass sie das folgende Summierproblem lösen.

Eingabe: zwei natürliche Zahlen m und n (z.B. 5 und 12)

Ausgabe: Summe aller Zahlen, die größer oder gleich m und kleiner als n sind (im Beispiel: 5+6+7+8+9+10+11)

(b) Entwickle ein Python-Programm mit einer while-Anweisung zur Lösung des Summierproblems.

(c) Teste auch das folgende Programm zur Lösung des Summierproblems. Wie wird hier die Zählung realisiert?

for-Anweisung in Python

Allgemein lässt sich eine for-Anweisung in Python wie folgt darstellen:

for [Element] in [iterierbares Objekt]:
    [Anweisungssequenz]

Eingeleitet wird sie mit dem Schlüsselwort for. Anschließend folgt ein Ausdruck der Form Element durchläuft ein iterierbares Objekte und ein Doppelpunkt. Der Doppelpunkt deutet darauf hin, dass jetzt die zu wiederholenden Anweisungen folgen. Diese Anweisungen müssen um eine feste Anzahl von Leerzeichen eingerückt werden. Hält man sich nicht an diese Einrücksystematik, so erhält man Fehlermeldungen oder auch fehlerhafte Programme.

Beispiele für iterierbare Objekte sind Zeichenketten, Tupel und Listen. Im Folgenden wird die Verwendung einer for-Anweisung zur Verarbeitung solcher Objekte anhand von Beispielen kurz angedeutet. Weitere Beispiele werden in den entsprechenden Abschnitten folgen.

Beispiel: Zeichenkette als iterierbares Objekt

Beispiel: Tupel als iterierbares Objekt

Beispiel: Liste als iterierbares Objekt

Der range-Operator in Python

Mit Hilfe des range-Operators lassen sich in Python iterierbare Objekte erzeugen, mit deren Hilfe dann Zählschleifen flexibel modelliert werden können. Betrachten wir erst zuerst einige Beispiele:

Beispiel: i = 0, 1, 2, 3, 4

Beispiel: i = 2, 3, 4, 5

Beispiel: i = 1, 3, 5

Beispiel: i = 4, 3, 2

Der range-Operator lässt sich also in drei Varianten verwenden:

• range(stop): Es werden alle Zahlen von 0 bis stop durchlaufen, ohne stop zu erreichen.
• range(start, stop): Es werden alle Zahlen von start bis stop durchlaufen, ohne stop zu erreichen.
• range(start, stop, step): Es werden alle Zahlen von start bis stop in step-Schritten durchlaufen, ohne stop zu erreichen.

Aufgabe 2

Benutze den range-Operator, um Summen ungerader Zahlen zu berechnen.

Eingabe: natürliche Zahl n

Ausgabe: Summe 1+3+5+...+(2n-1)

Wenn man beispielsweise die Zahl 4 eingibt, dann soll man die Ausgabe 16 (= 1+3+5+7) erhalten.

Fällt dir dabei etwas auf? Tipp: Quadrieren