Primzahlen

Von Mathematiker sehr geschätzt

Primzahlen sind natürliche Zahlen größer als 1, die nur durch 1 und sich selbst (ohne Rest) teilbar sind.

Beispiele:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ...

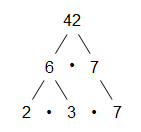
Primzahlen können als Bausteine der natürlichen Zahlen angesehen werden. Jede natürliche Zahl größer als 1 lässt sich als Produkt von Primzahlen darstellen.

Primzahlen haben viele faszinierende Eigenschaften. So kann man leicht zeigen, dass es unendlich viele Primzahlen gibt.

Es gibt auch noch viele ungelöste Fragen im Zusammenhang mit Primzahlen. So weiß man z.B. noch nicht, ob es auch unendlich viele Primzahlzwillinge (das sind aufeinander folgende Primzahlen wie 5, 7 oder 11, 13) gibt.

Von Nicht-Mathematikern meist unterschätzt

Die Beschäftigung mit Primzahlen gilt für Nicht-Mathematiker als eher unnützer Zeitvertreib. Dabei sind Primzahlen heutzutage wichtige Akteure, wenn es um Sicherheit bei der Kommunikation im Internet geht. Unsere Sicherheitsinfrastruktur beruht in zentralen Punkten auf den Eigenschaften von Primzahlen. Mehr hierüber findest du im Kapitel Das RSA-Verfahren.

Zielsetzung

Wir werden im Folgenden Funktionen zur Erzeugung von Primzahlen und zur Untersuchung von Primzahleigenschaften entwickeln. Dabei steht die korrekte Beschreibung von komplexeren Berechnungsabläufen im Vordergrund.