Modellierung einer Mäusepopulation
Beschreibung der Fortpflanzung einer Mäusepopulation
Mäuse pflanzen sich bekanntlich sehr rasch fort.
Im Folgenden soll die Entwicklung einer Mäusepopulation untersucht werden. Differenzierte Ergebnisse erhält man, wenn man die Population in Altersklassen aufteilt. Hier bietet sich eine grobe Aufteilung in junge, erwachsene und alte Mäuse an.
Ein einfaches Fortpflanzungsmodell
Wir betrachten das folgende einfache, an wissenschaftlichen Modellen angelehnte, Fortpflanzungsmodell.
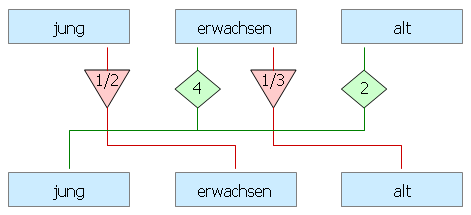
- In jedem Schritt erfolgt ein Wechsel der Altersklasse: Junge Mäuse werden erwachsen, erwachsene werden alt (und alte Mäuse leider nicht mehr jung). Allerdings werden nicht alle jungen Mäuse erwachsen. Nur ein bestimmter Anteil, der nach dem Diagramm genau die Hälfte beträgt, erreicht die nächste Altersstufe. Die anderen Mäuse sterben (leider). Ebenso werden laut Diagramm nur ein Drittel der erwachsenen Mäuse auch wirklich alt.
- Im Diagramm sind zusätzlich die Geburtenraten eingetragen. Wir gehen davon aus, dass in jedem Schritt jede erwachsene Maus im Durchschnitt vier junge Mäuse erzeugt und dass jede alte Maus im Durchschnitt zwei junge Mäuse erzeugt.
Berechnungen zur Populationsentwicklung
Wir beginnen mit Berechnungen zur Populationsentwicklung. Den Computer benutzen wir vorerst noch nicht. Die hier berechneten Werte dienen später als Kontrollwerte.
Aufgabe 1
Wenn zu Beginn der Simulation 6 junge, 9 erwachsene und 12 alte Mäuse leben, dann pflanzt sich diese Population wie folgt fort:
| Schritt | jung | erwachsen | alt |
|---|---|---|---|
| 0 | 6 | 9 | 12 |
| 1 | 9*4+12*2=60 | 6:2=3 | 9:3=3 |
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Berechne die fehlenden Populationswerte. Zur Kontrolle: Nach 5 Schritten besteht die gesamte Population aus knapp 300 Mäusen.
Du kannst deine Ergebnisse auf folgendem Arbeitsblatt festhalten:
Quellen
- [1]: Foto mit Mäusen - Urheber: Kessa Ligerro - Lizenz: Creative Commons BY-SA 3.0


